Randomly generate scales on a flat — populate

Sometimes it's useful to explore a flat or a color by testing small differences that result from different positions within the flat. This function generates random points on the desired flat to test, similar to surround_set() but constrained to lie on a target flat. Requires a base set that serves as an "origin" around which the random scales are to be generated (before being projected onto the target flat).

Usage

populate_flat(
  set,
  target_scale = NULL,
  target_rows = NULL,
  start_zero = TRUE,
  ineqmat = NULL,
  edo = 12,
  rounder = 10,
  magnitude = 2,
  distance = 1
)

Arguments

set: Numeric vector of pitch-classes in the set
target_scale: A numeric vector which represents a scale on the target flat.
target_rows: An integer vector: each integer specifies a row of ineqmat which helps to determine the target flat. The rows must be linearly independent.
start_zero: Boolean: should the result be transposed so that its pitch initial is zero? Defaults to TRUE.
ineqmat: Specifies which hyperplane arrangement to consider. By default (or by explicitly entering "mct") it supplies the standard "Modal Color Theory" arrangements of getineqmat(), but can be set to strings "white," "black", "gray", "roth", "infrared", "pastel", "rosy", "infrared", or "anaglyph", giving the ineqmats of make_white_ineqmat(), make_black_ineqmat(), make_gray_ineqmat(), make_roth_ineqmat(), make_infrared_ineqmat(), make_pastel_ineqmat(), make_rosy_ineqmat(), make_infrared_ineqmat(), or make_anaglyph_ineqmat(). For other arrangements, this parameter accepts explicit matrices.
edo: Number of unit steps in an octave. Defaults to 12.
rounder: Numeric (expected integer), defaults to 10: number of decimal places to round to when testing for equality.
magnitude: Numeric value specifying how many sets to return. Defaults to 2.
distance: How far (in units of voice leading work, using the Euclidean metric) should the sampled scales be from the input set?

Value

A matrix whose columns represent scales on the desired flat. The matrix has n rows (where n is the number of notes in set) and n * 10^magnitude columns.

Details

The target flat can be specified by naming the target_rows that determine the flat (in the manner of project_onto()) or by naming a target_scale on the desired flat. Both parameters default to NULL, in which case the function populates the flat that set itself lies on.

Examples

# Let's sample several scales on the same flat as j(dia):
major <- c(0, 2, 4, 5, 7, 9, 11)
jdia_flat_scales <- populate_flat(major, j(dia))
unique(apply(jdia_flat_scales, 2, whichsvzeroes), MARGIN=2)
#>       [,1]
#>  [1,]    4
#>  [2,]    8
#>  [3,]   11
#>  [4,]   14
#>  [5,]   18
#>  [6,]   23
#>  [7,]   25
#>  [8,]   30
#>  [9,]   33
#> [10,]   37
#> [11,]   38
#> [12,]   41

# So all the scales do lie on one flat, but they may be different colors.
# Let's plot them using different literal colors to represent the scalar "colors."
jdia_flat_svs <- apply(apply(jdia_flat_scales, 2, signvector), 2, toString)
unique_svs <- sort(unique(jdia_flat_svs))
match_sv <- function(sv) which(unique_svs == sv)
sv_colors <- grDevices::hcl.colors(length(unique_svs), 
                                   palette="Green-Orange")[sapply(jdia_flat_svs, match_sv)]
plot(jdia_flat_scales[2,], jdia_flat_scales[3,], pch=20, col=sv_colors,
  xlab = "Height of scale degree 2", ylab = "Height of scale degree 3",
  asp=1)
abline(0, 2, lty="dashed", lwd=2)
points(j(2), j(3), cex=2, pch="x")
points(2, 4, cex=2, pch="o")


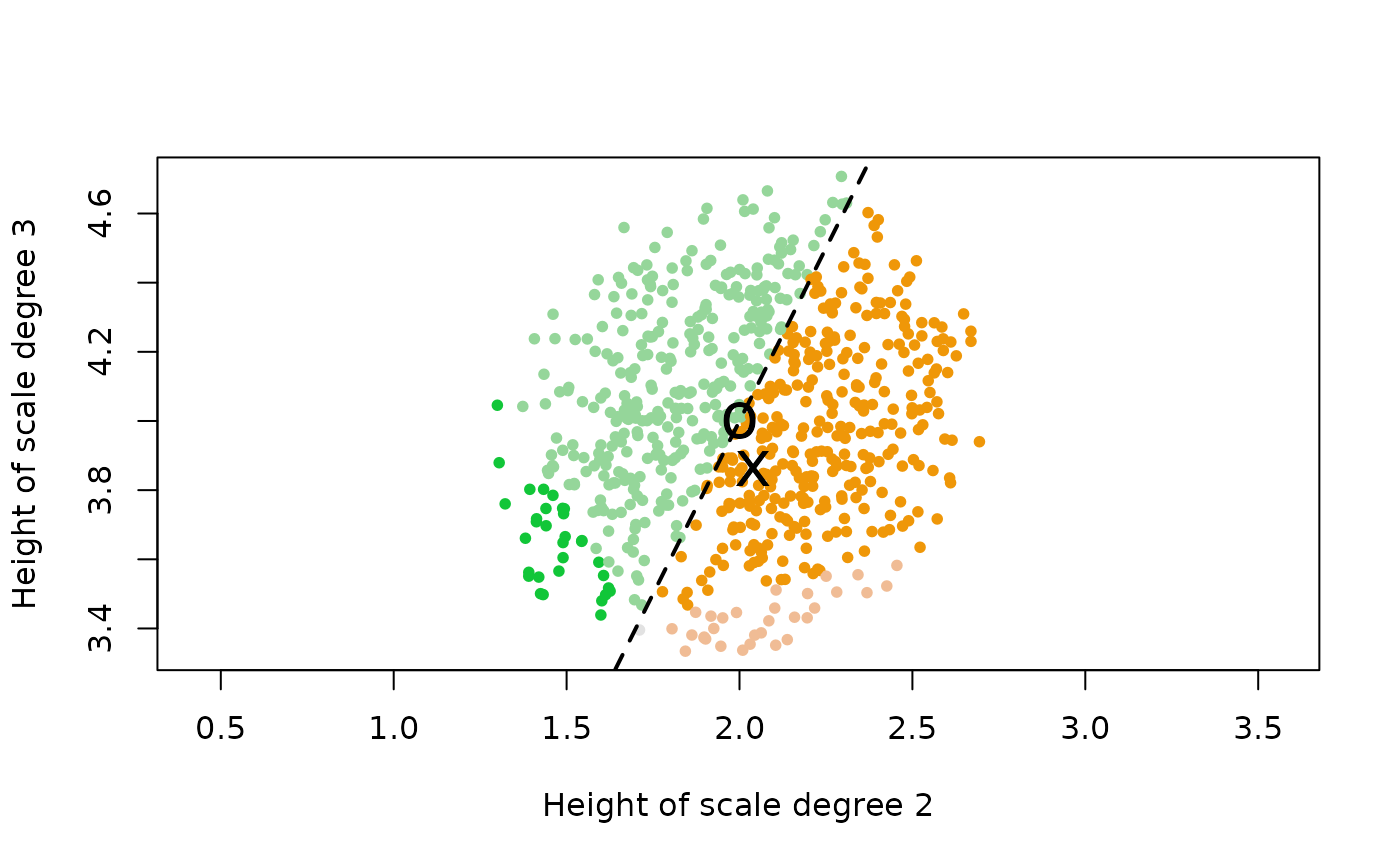# Most of our sampled sets belong to two colors separated by the dashed
# line on the plot. The dashed line represents the inequality that determines 
# the size of a scale's second step in relation to its first step. This is
# hyperplane #1 in the space, so it corresponds to the first entry in each 
# scale's sign vector. The point labeled "x" represents the just diatonic scale 
# itself, which has a larger first step than second step. The point labeled 
# "o" represents the 12-equal diatonic, whose whole steps are all equal and which 
# therefore lies directly on hyperplane #1. Finally, note that our sampled scales
# also touch on a few other colors at the bottom & left fringes of the scatter plot.