Symmetries of hyperplane arrangements define equivalent scales

Produces scales of different colors which have equivalent scalar properties. The hyperplane arrangements of MCT have three types of symmetry, which allows us to find scales at different but equivalent points in the arrangement. Such scales will be nearly structurally identical in most senses although their specific intervals will be rather different. See details for a discussion of the symmetries involved.

Usage

ineqsym(set, a = 1, b = 0, involution = FALSE, edo = 12)

Arguments

set

Numeric vector of pitch-classes in the set

a

Integer: controls permutations of generic intervals. Must be coprime to the size of the set. Defaults to 1.

b

Integer: controls modal rotation. Defaults to 0.

involution

Boolean: controls involutional symmetry. Defaults to FALSE.

edo

Number of unit steps in an octave. Defaults to 12.

Value

Numeric vector representing a scale of same length as set. Default parameters determine the identity symmetry and will return set itself.

Details

Two symmetries of the MCT hyperplane arrangement are familiar. One is modal "rotation": two modes of the same scale must have equivalent structures, by the defining relations of the theory. The parameter b controls these rotations. The second familiar symmetry is involution (see "Modal Color Theory," 32). Set parameter involution to TRUE to apply this symmetry. The more interesting symmetry of the MCT arrangements is controlled by parameter a. This symmetry allows us to permute the roles of the scale's generic intervals in its scalar makeup. For instance, non-degenerate well-formed scales (see iswellformed() are all generated by a particular generic interval. The familiar diatonic scale is generated by its generic fourths, whereas another well-formed scale like (0, 2, 3, 5, 6, 7, 9) in 10edo (with step-word LSLSSLS) is generated by its generic sixths. We can permute the hyperplanes of the heptachordal MCT arrangement so that the overall structure is preserved but the diatonic scale is mapped onto LSLSSLS. In general, the permutations of ineqsym() allow us to map any non-degenerate well-formed scale onto any other: they form an orbit under the symmetries of the space. This gives another sense in which "well-formedness" is a large family of scale structures. That sense generalizes to all scales, not just ones that are highly regular like well-formed scales.

In short, ineqsym() preserves many scalar properties, including:

• countsvzeroes() and svzero_fingerprint()

• howfree()

• ratio(), delta(), and eps()

• brightnessgraph() structure

• evenness()

• isgwf() and a fortiori iswellformed()

• Number and respective properties of adjacent colors

• spectrumcount() up to permutation of the values

Examples

wt_plus_1 <- sc(7,33)
equiv_scale <- ineqsym(wt_plus_1, 3, 2)
both_scales <- cbind(wt_plus_1, equiv_scale)
freedoms <- apply(both_scales, 2, howfree)
evennesses <- round(apply(both_scales, 2, evenness), 3)
svzeroes <- apply(both_scales, 2, countsvzeroes)
ratios <- round(apply(both_scales, 2, ratio), 3)
spectra <- apply(apply(both_scales, 2, spectrumcount), 2, toString)
cbind(freedoms, evennesses, svzeroes, ratios, spectra)
#>             freedoms evennesses svzeroes ratios spectra           
#> wt_plus_1   "1"      "1.195"    "16"     "1.5"  "2, 3, 3, 3, 3, 2"
#> equiv_scale "1"      "1.195"    "16"     "1.5"  "3, 2, 3, 3, 2, 3"
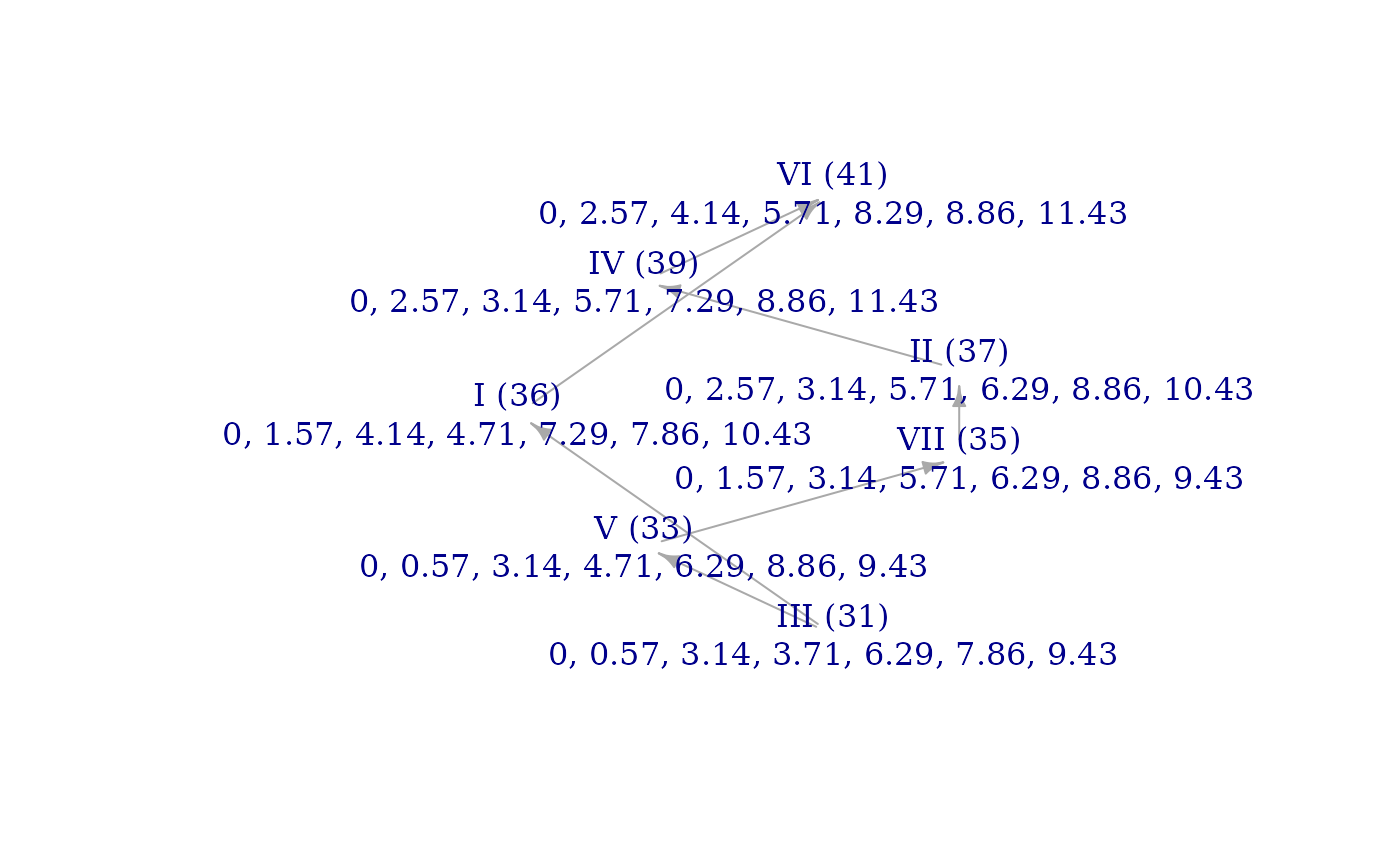
brightnessgraph(wt_plus_1)

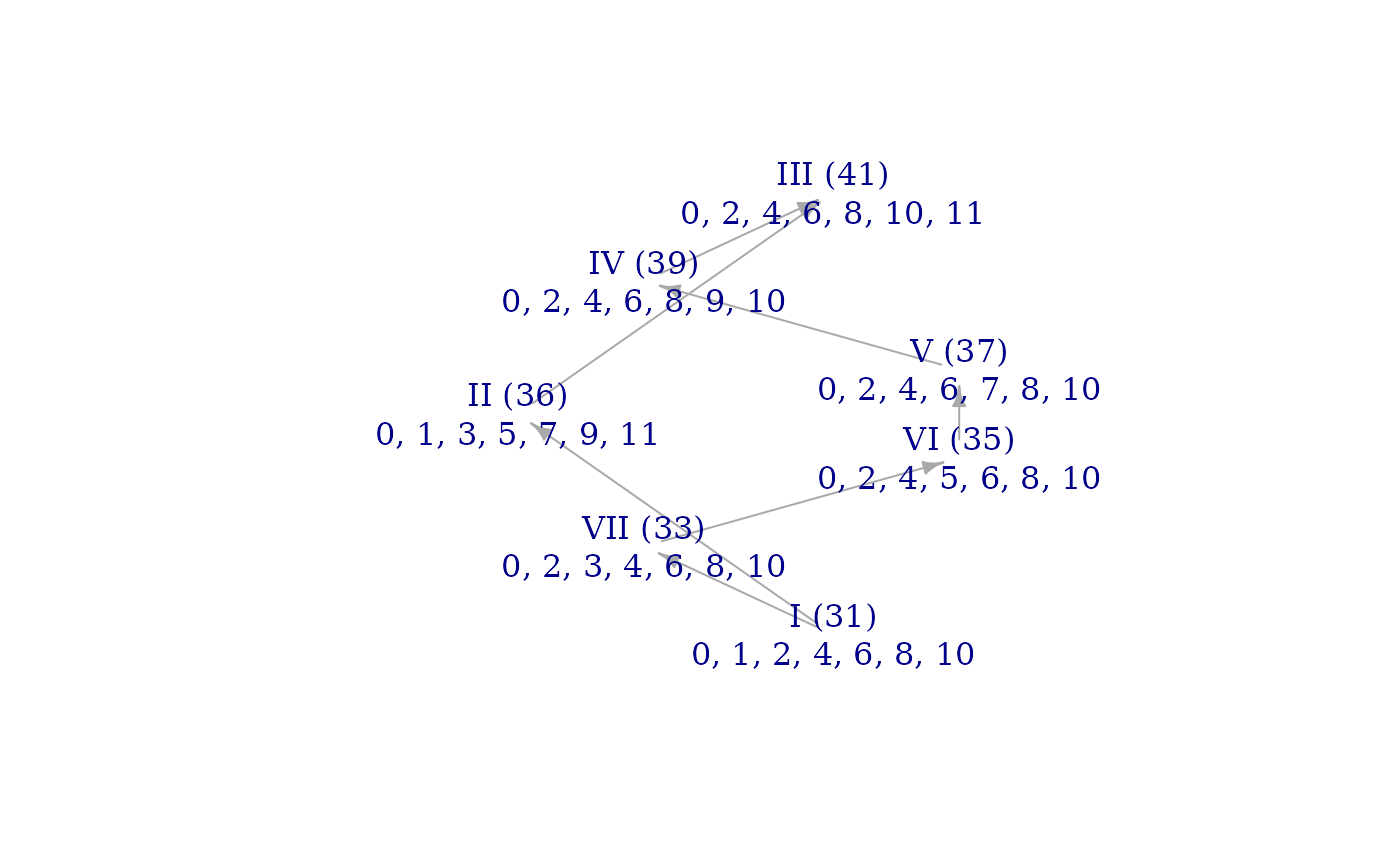brightnessgraph(equiv_scale)